2-1. 地球の形をどのように記載するか
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
2-1-1. 地球概観-地球の形(*)
地球は球形に近い. 古代ギリシャ人は, すでにその事実を認識していた. 球としての地球の大きさが初めて測定されたのは, 紀元前3世紀のエジプトにおいてである. そのとき, エラトステネスが求めた円周の長さは, 現在の値よりわずか15%大きいだけである.
17~18世紀には, 地球の形が赤道方向に張り出した扁平な楕円体か, 南北に長いたて長の楕円体かをめぐり, ニュートンとカッシーニとの間で国際的論争が起こった. フランス学士院は南米エクアドルとスカンジナビア半島で緯度差$1^\circ$あたりの弧長を測定し, 地球が扁平な回転楕円体であることを証明した.
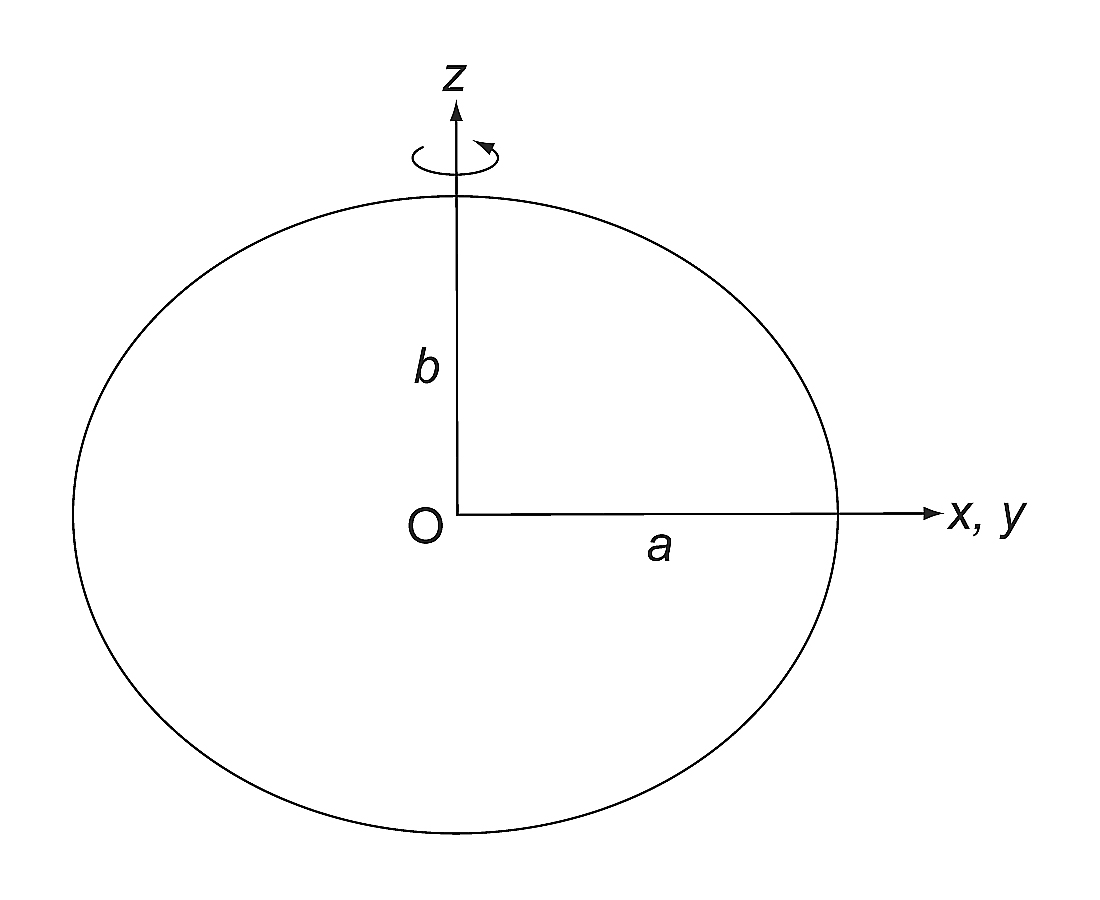
19世紀から現在まで, 三角測量, 重力測量, 人工衛星の軌道解析などの結果をもとに, 現実の地球の形状に最も近い回転楕円体, すなわち地球楕円体が求められてきた. 回転楕円体の形状は赤道半径$a$と極半径$b$で決まる(図1). 一般には, $b$ の代わりに, $f=(a-b)/a$ で定義される扁平率$f$を用いる. 概略値は$a$が約6,378km, $f$が約1/300である. 肉眼では, 扁平率が約1/300の回転楕円体を球と区別することはできない. 一方, 現実の地球では$a-b$の値は約21kmとなる. 測地学において, これは非常に大きな値である. 扁平率1/300のわずかなつぶれ方が, 地球に対しさまざまな現象をひき起こす.
現実の地球の表面には細かな凹凸があり, 内部の質量分布も均一ではない. その結果, 重力の大きさと向きは, 場所ごとにわずかに異なる. 地球楕円体は数学的に厳密に定義できるが, 局所的な地形の凹凸や重力分布を無視している. 地球上で生活するものにとって, 最も身近な基準は, 重力の方向とそれに直交する水平面である. 物理学的には, 水平面は重力の等ポテンシャル面のひとつと定義できる. 地球の形状を最も良く近似する等ポテンシャル面がジオイドである. ジオイドは地球内部の質量分布を反映しており, 地球楕円体面に対して凹凸がある(ジオイド高).
図1. 長半径$a$, 短半径$b$の回転楕円体
2-1-2. 地球概観-地球の内部構造(**)
地球の内部構造は, 主に20世紀に入ってから, 地震波の解析によって明らかにされた. 地震波には速度の異なるP波(縦波)とS波(横波)がある. P波, S波とも, 速度は媒質の密度と弾性定数の関数で, 地球内部でこれらが変化することにより, 地震波の屈折や反射が起こる. また, S波は流体中を伝播しない. 一般に, 深さ方向に速度が変化する層構造を仮定し, 震源からの距離に対して地震波の伝播に要した時間(走時)の関係を用いて, 層の厚さと層内の地震波速度を推定する.
20世紀初頭, モホロビチッチは地表から約50kmの深さに速度の明瞭な不連続を発見した. これが地殻とマントルの境界(モホロビチッチ不連続面: モホ面)である. 後に, 震源からの角距離が103$^\circ$~143$^\circ$の領域に地震波が到達していないこと, さらに, S波は143$^\circ$より遠方にも到達していないことが発見された. これより, 地表から2900kmより深部に流体の核が存在することが推定された. この核‐マントル境界(Core-Mantle Boundary: CMB)で反射した地震波が明瞭に観測されることから, 境界をはさんで地震波速度の変化は急激である. その後の詳細な解析により, 核は, 流体からなる外核と, 半径1220kmの固体からなる内核とに分かれていることも明らかになった(図2).
世界中の地震データを解析して, ジェフリーズとグーテンベルグはそれぞれ別個に地球の地震波速度モデルを確立した. 2つのモデルに大きな差は無く, わずかな違いは, グーテンベルグモデルは地表から100~200kmの深さに速度のわずかな極小を持つのに対し, ジェフリーズモデルにはこれが存在しないことである.
地震波速度構造と異なり, 地球内部の密度分布を直接決定する方法はない. ブレンはジェフリーズの地震波速度モデルを用い, 圧力変化と密度変化との間に適当な仮定を設けて, 地球内部の密度と弾性定数の分布を求めた. 竹内均は, このモデルに月と太陽の引力が作用したときの理論的な地球潮汐応答を計算し, モデルの妥当性を証明した. すなわち, 地震波と地球潮汐という周波数の大きく異なる2つの現象から, 地球の流体核の存在が証明された.
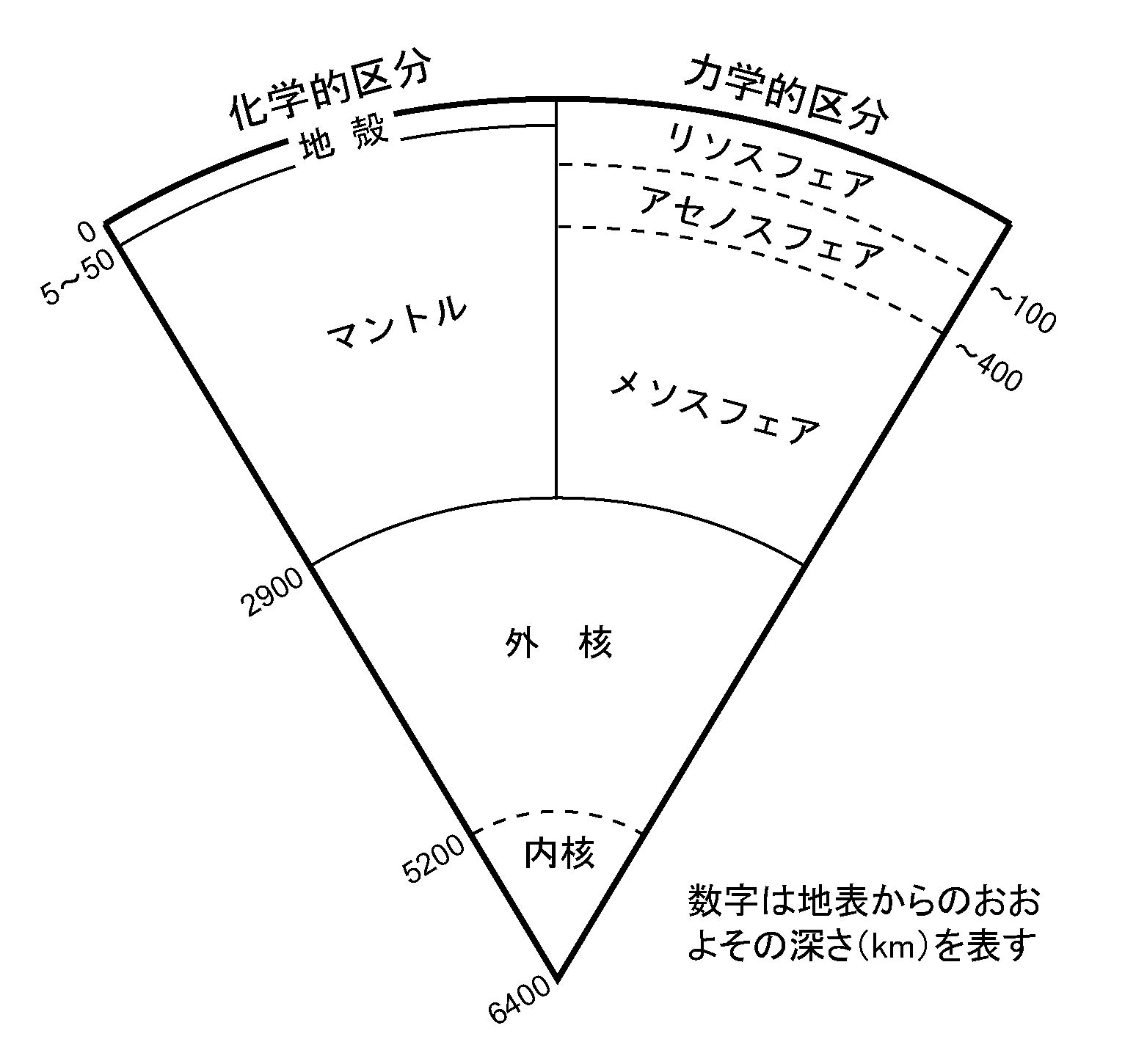
図2. 地球内部の層区分. 構成物質や化学組成の違いに基づいた化学的区分と, 外力に対する応答に基づいた力学的区分とは一致しない.
2-1-3. 地球楕円体(*)
地球上の位置を経度, 緯度, 高さで表すには, まず基準を設定する必要がある. 地表は複雑な起伏を持ち, しかも地殻変動や侵食, 堆積により, 長期間でその形状が変化する. 一方, 重力の等ポテンシャル面であるジオイドは, 数学的に厳密な定義が可能である. しかし, 地球内部の質量分布の不均質を反映して, 実際の地形ほどではないにしても, やはり凹凸を持つ. 地表やジオイドは, 地球上の位置をくまなく表す基準としては複雑すぎる.
地球の形状に最も近い幾何学的立体は, 楕円をその短軸の回りに回転させた回転楕円体である(図1). そこで, 地球の形状を最も良く代表する回転楕円体を決定し, これを地球楕円体と呼ぶ.
地球楕円体の形を決定するものは赤道半径a と扁平率f である. 極半径b , 離心率e との間に$f=(a-b)/a$, $e^2=(a^2-b^2)/a^2$の関係がある. これらの値は, 従来は, 測地測量と重力測量の結果に基づいて決められてきた. 最新の地球楕円体である測地基準系1980(Geodetic Reference System 1980:GRS80)は, 人工衛星の軌道解析に基づいている. そのため, 地球の自転速度や重力ポテンシャルに関する定数も同時に定義されている.
注意すべきことは, 地球楕円体が精度良く決定されたとしても, それを実際の地球にあてはめる際に, 無数の方法が存在することである(図3). 地球楕円体の中心を地球の重心に一致させた座標系は, 地心座標系と呼ばれる. 平均的に現実の地球の形状を代表するものの, 一致度の良い地域とそうでない地域が混在する. 一方, 地表の特定の位置(測地原点)において楕円体を地球に固定したものは, 局所座標系と呼ばれる. それが利用される範囲内で楕円体は実際の地球に良く一致するが, 楕円体の中心と地球の重心は一致せず, また, その地域外での一致度は一般に良くない. 採用される楕円体も, 国や地域によって同一とは限らない. このように, ある特定の位置に取り決めによって設定された楕円体を準拠楕円体と呼ぶ.
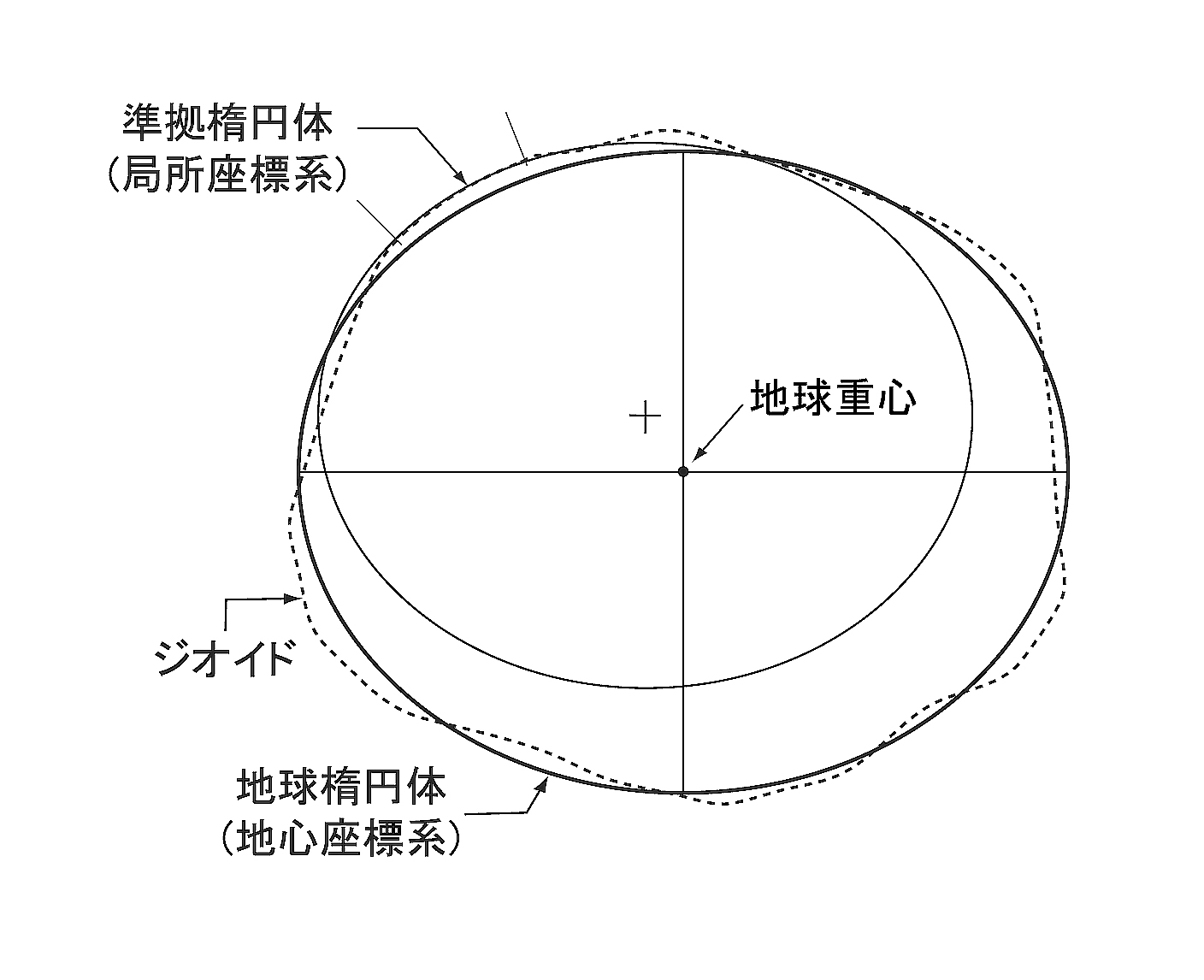
図3. 地心座標系と局所座標系. 回転楕円体を地球の外形(ジオイドで代表される)にあてはめる方法はひとつではない. 地心座標系では原点は地球重心に一致する. 局所座標系では原点と地球重心が一致しないが, 特定の地域へのあてはめ方が最良となる.
2-1-4. 日本測地系(**)
2002年4月1日に測量法が改正され, 日本の測地座標系(日本測地系)の定義が大きく変更された. 新しい測地系は地心座標系, 従来の系は局所座標系である.
新しい測地系を設定するには, まず, 東京都港区にある測地原点(経緯度原点)の位置をGPS, VLBI等の宇宙測地技術によって精度良く決定する. このとき用いられる座標系は, ITRF(International Terrestrial Reference Frame, 国際地球基準座標系)という, 座標原点を地球重心に置いた3次元直交座標系である. 次に, 経緯度原点のxyz座標を, 測地基準系1980を基準とした経度, 緯度, 高さに変換する. このとき, 楕円体の中心は地球重心に一致させる. こうして, 経緯度原点の経度, 緯度, 高さが, 地心座標系に基づいて表現される.
以上で, 水平位置だけでなく高さ(楕円体高)も定義される. しかし, GPSやVLBIと違い, 水準測量によって決まる従来の高さ(標高)は, ジオイドを基準にしており, 楕円体を基準にしたものではない. 高さの定義が急に変更されると, 大きな混乱を生じる. そこで, 新しい測量法も, 高さに関しては従来と同じ定義を踏襲している. つまり, 東京都千代田区にある水準原点の高さを24.4140m(*注)と定義する.
従来の日本測地系を設定するには, まず, 経緯度原点を通る鉛直線を, ベッセル楕円体上で原点と同じ経度, 緯度の点に立てた垂線と一致させる. このときの経緯度原点の経度, 緯度, 鉛直線の方向は, 天文観測により決定された. 次に, 原点から千葉県鹿野山の三角点を見た方位を原点方位角と定める. 最後に, 水準原点の直下24.4140mをベッセル楕円体面が通過しているとする. つまり, 高さの基準とした東京湾平均海面が, ここでベッセル楕円体面と一致しているとみなしている.
日本測地系の改正に伴う経緯度原点の見かけの移動は, 北西方向へ約450mである(図4).
*注:平成23年東北地方太平洋沖地震の変動により, 現在は24.3900mと改められている.
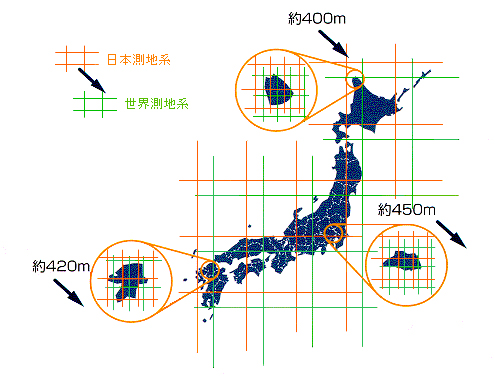
図4. 測地系の移行に伴う座標の移動(国土地理院のホームページ内「世界測地系移行の概要」の紹介ページより).
2-1-5. 3次元直交座標系(**)
地球上の位置を経度, 緯度, 高さで表すには, 地球楕円体を基準にする. その楕円体の形状は, 3次元直交座標系を用いれば, 比較的簡単に, かつ厳密に記述することができる. したがって, 原点を地球重心に持ち, 地球とともに回転する3次元直交座標系(地球基準座標系)を定義しておくと, 楕円体を基準に位置を表現する際にも, 何かと便利である. また, 楕円体面のはるか上空を運動する人工衛星の位置は, 楕円体を基準とするより, 直交座標系で表すほうがより自然である. 最近の位置決定手法の主流となっているGPS, VLBI, SLRなどの宇宙測地技術も, 直交座標系であるITRFを基準としている. つまり, 最近は, 位置の直交座標3成分が先に決定され, 直交座標系と楕円体の関係式を用いて経度, 緯度, 高さに変換される, というケースが一般的になりつつある.
直交座標系xyz系を地球に固定するには, x, y軸を赤道面内にとり, z軸を地球の自転軸に一致させる. x軸はグリニッジ子午線と赤道との交点の方向にとり, これより東回りに東経を, 西回りに西経を計る. y軸は赤道面内で東経90$^\circ$の方向にとる(図5).
地球上で生活するものにとって地球基準座標系は便利であるが, この系は地球とともに回転しており, 厳密にはニュートンの慣性の法則が成り立たない非慣性座標系である. 一方, 天体や人工衛星の運動は, 宇宙空間に固定された慣性座標系でのみ厳密に記述することができる. これらを地球基準座標系に変換するには, 宇宙から見た地球回転運動を知らねばならない. これには, 歳差, 章動, 極運動といったものが含まれる. 宇宙測地データの解析ソフトウェアにはこれらの運動モデルが内蔵されているが, より高度な解析には, 全地球規模の実測データに基づいた地球回転情報が必要である.
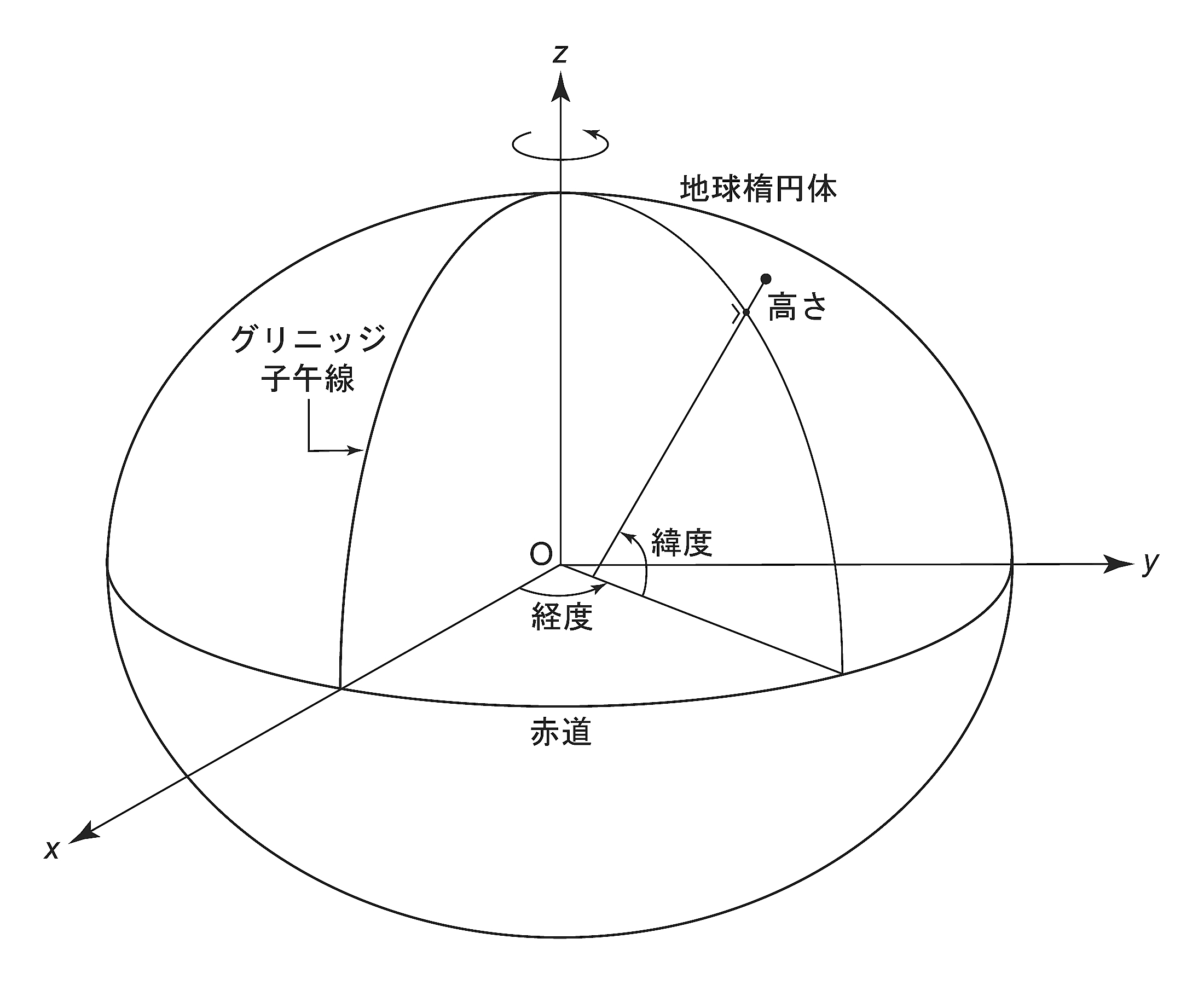
図5. 地球重心に原点を持つ3次元直交座標系と, 地球楕円体を基準とした経度, 緯度, 高さ.
2-1-5-1. ITRF(***)
ITRF(International Terrestrial Reference Frame, 国際地球基準座標系)は, GPS, VLBI, SLRなどの宇宙測地観測データに基づいて国際地球回転事業(International Earth Rotation and Reference Systems Service:IERS)が提供する, 3次元直交座標系である. GPS衛星の精密軌道はITRFで表現されている.
地球上のすべての観測点は, いずれかのプレート上に位置している. プレートは地球深部に対して運動しており, さらに, プレート境界周辺ではプレートの内部変形が生じている. 従って, 地球上に不動の観測点は存在しない. 任意の時刻の観測点位置を求めるには, ある時刻における観測点位置(初期位置)と, その後の移動速度を知らなければならない. 座標のx成分を例にとると, 時刻$T_0$における初期位置を$X_0$, 速度を$V_x$とすれば, 時刻$T$における位置$X(T)$は$X(T)=X_0+V_x(T-T_0)$となる. ITRFの表には, 観測点の初期位置と速度が, 推定誤差とともに掲載されている.
ITRFの実現には, 世界中に分布した観測点で, 十分な期間のデータを取得する必要がある. こうした条件が整ったのは, 1990年代以降である. その後, 観測点の新設とデータの蓄積が進み, ITRFは何回も改訂されている. ITRFの最新版であるITRF2008に位置と速度が登録されているものは, GPS観測点だけで500に達する. 座標系の地球へのあてはめ方や, 観測点の初期位置と速度も, 改訂ごとに, より正確になっている.
ITRFでは観測点の位置だけでなく速度も重要であるが, それは何に対する速度だろう? ITRFはNNR-NUVEL1Aというプレート運動モデルに準拠している. 地球深部に対する絶対座標系と考えて差し支えない. 特定のプレートに対する速度に変換するには, 3次元直交座標で表された速度成分を東西, 南北, 高さ成分に変換した後, NNR-NUVEL1Aを用いて, 基準にしたいプレートの絶対運動を差し引く.
2-1-6. 緯度・経度(*)
地球楕円体と3次元直交座標系を考える. 図6において, 極軸(z軸)を通る面を子午面, 楕円体と子午面との交線を子午線という. とくに, 英国グリニッジ天文台を通る子午線をグリニッジ子午線という. ある点を通る子午面がグリニッジ子午面となす角が経度である. 東回りに東経を, 西回りに西経を計る. また, 子午線と直交する大円を卯酉線(ぼうゆうせん)と呼ぶ. 子午線, 卯酉線の名前は, 十二支で方向を表したとき, 子(北), 卯(東), 午(南), 酉(西)の方向の呼び名に由来する.
赤道半径$a$, 極半径$b$の回転楕円体は,
\[ \frac{(x^2+y^2)}{a^2}+\frac{z^2}{b^2}=1 \tag{1} \]
で表される(図7). 楕円体上に点$P(x, y, z)$をとり, 中心$O$からの距離を$r$, $OP$が赤道面となす角を$\phi$, 経度を$\lambda$とすると,\[ x=r\cos\phi\cos\lambda, y=r\cos\phi\sin\lambda, z=r\sin\phi \tag{2} \]
の関係がある. $\phi$を地心緯度と呼ぶ. 一方, 点$P$において楕円体に立てた垂線が極軸と交わる点を$Q$とし, $QP$の長さを$N$, $QP$が赤道面となす角を$\psi$とすると,\[ x=N\cos\psi\cos\lambda, y=N\cos\psi\sin\lambda, z=\frac{b^2}{a^2}N\sin\psi \tag{3} \]
となる. $\psi$を測地緯度(地理緯度)と呼ぶ. $\phi$と$\psi$の間には,\[ \tan\phi=\frac{b^2}{a^2}\tan\psi \tag{4} \]
の関係がある. さらに,\[ r=\frac{b}{\sqrt{(1-e^2\cos^2\phi)}}, N=\frac{a}{\sqrt{(1-e^2\sin^2\psi)}} \tag{5} \]
となる. $e (= (a^2-b^2)^{1/2}/a )$は離心率である.もし, 点$P$が楕円体上でなく, 高さ(楕円体高)$H$の位置にある場合は,
\[ x=(N+H)\cos\psi\cos\lambda, y=(N+H)\cos\psi\sin\lambda, z=\left(\frac{b^2}{a^2}N+H\right)\sin\psi \tag{6} \]
となる. $(x,y,z)$が既知のとき, $\lambda$は$\tan\lambda=y/x$によって求めることができるが, $\psi$と$H$を求める問題は単純ではない. 一般に, ある初期値に対する補正量を求め, 補正された初期値を使った反復計算により, さらに近似を高めていく手法が用いられる.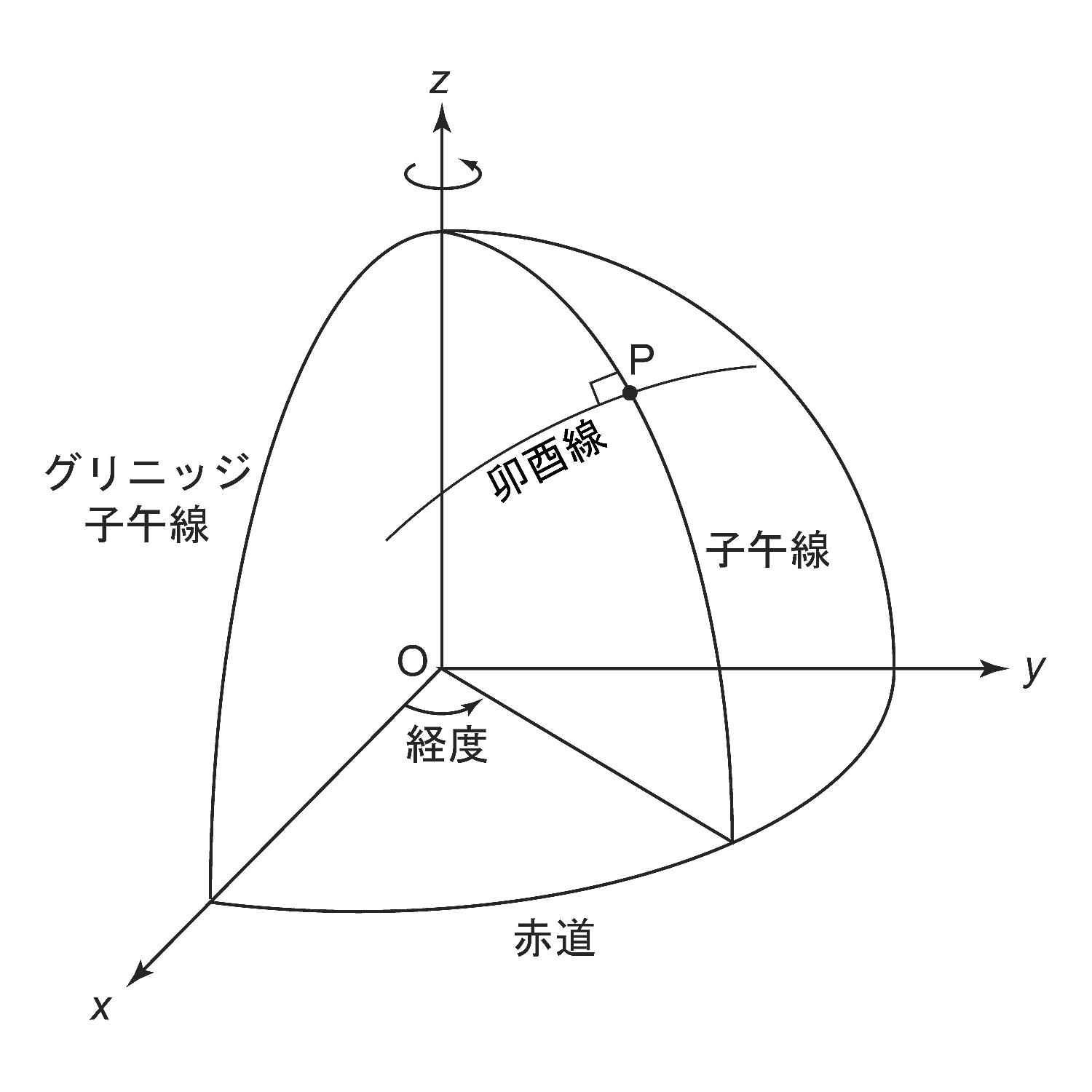
図6. 子午線, 経度, 卯酉線.
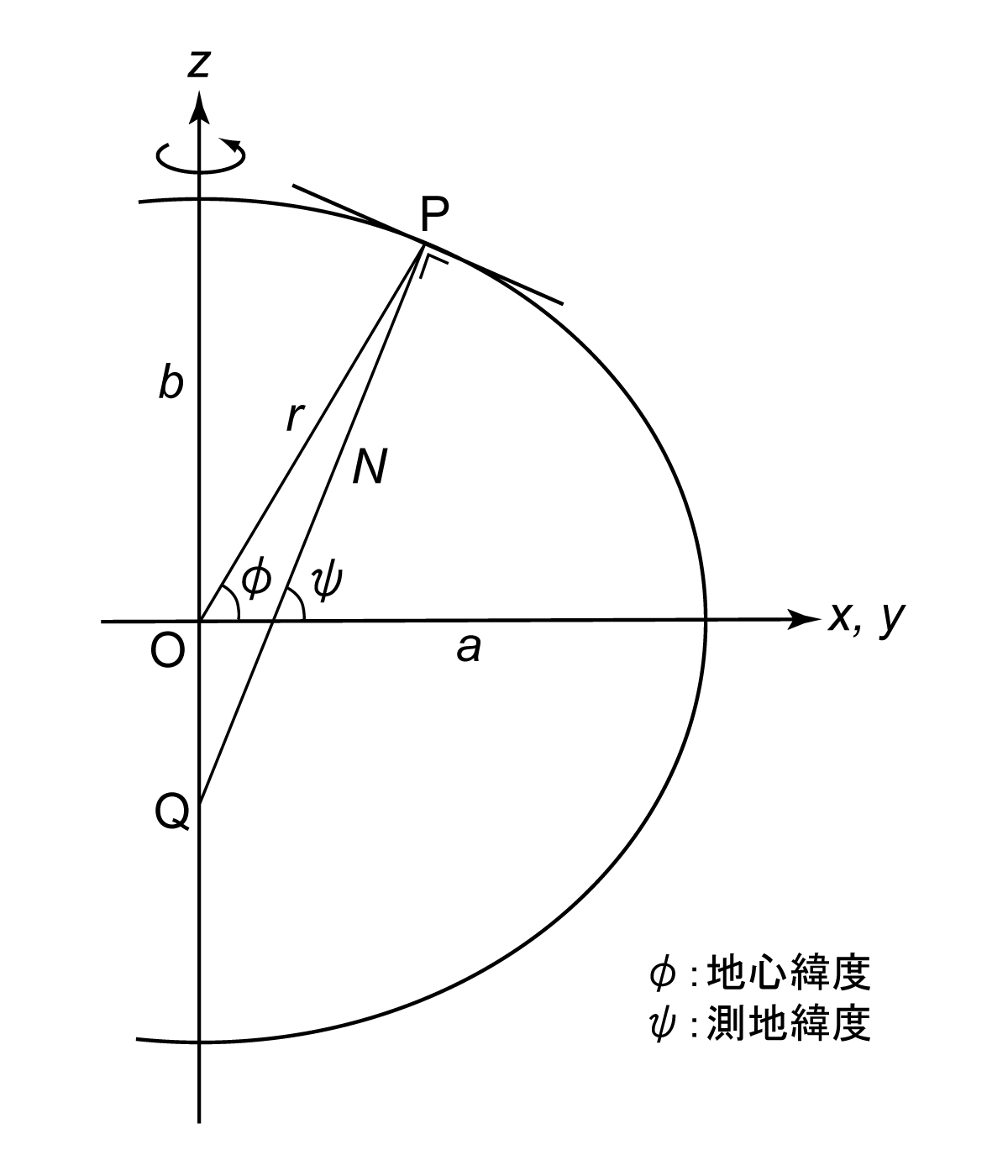
図7. 測地緯度(地理緯度)と地心緯度.
2-1-6-1. 天文緯度・経度(**)
あらかじめ天空上の位置がわかっている恒星を天文観測することにより, 観測点の緯度(天文緯度)と経度(天文経度)を決定することができる.
地球の赤道面から測った高度角(赤緯)$\delta$が既知である恒星が観測点を通る子午線を通過するとき, 天頂から恒星までの角度(天頂距離)$\zeta$と観測点の天文緯度$\phi^*$との間には$\phi^* =\delta \pm \theta$の関係がある. 恒星が天頂より南側を通過するときはプラスの符号を, 北側を通過するときはマイナスの符号をとる.
天文経度$\lambda^*$を決定するには, 恒星が子午線を通過する時刻を測ればよい. この時刻と, 恒星がグリニッジ子午線を通過する時刻との差から, 2つの子午線のなす角, すなわち経度が求められる.
ここで注意すべきことは, 天文観測の基準となるのは天頂方向であり, 重力の方向が楕円体に垂直でない場合には, その影響が観測結果に含まれることである. 重力の等ポテンシャル面に立てた垂線(鉛直線)は常に重力の方向に一致する. しかし, 地球内部の質量分布が均質でないために, 一般に等ポテンシャル面は楕円体面に一致しない. つまり, 鉛直線は楕円体に立てた垂線(垂直線)の方向に一致しない(図8). 鉛直線を基準にした垂直線のずれを垂直線偏差, 垂直線を基準にした鉛直線のずれを鉛直線偏差と呼ぶが, 両者の差は実用上無視して差し支えない.
楕円体を基準とした測地測量によって得られた緯度$\phi$, 経度$\lambda$と天文緯度$\phi^*$, 天文経度$\lambda^*$との差は鉛直線偏差(または垂直線偏差)を表す. その南北, 東西成分はそれぞれ,
\[ \zeta=\phi^{\ast}-\phi, \eta=(\lambda^{\ast}-\lambda)\cos\phi \tag{7} \]
となる.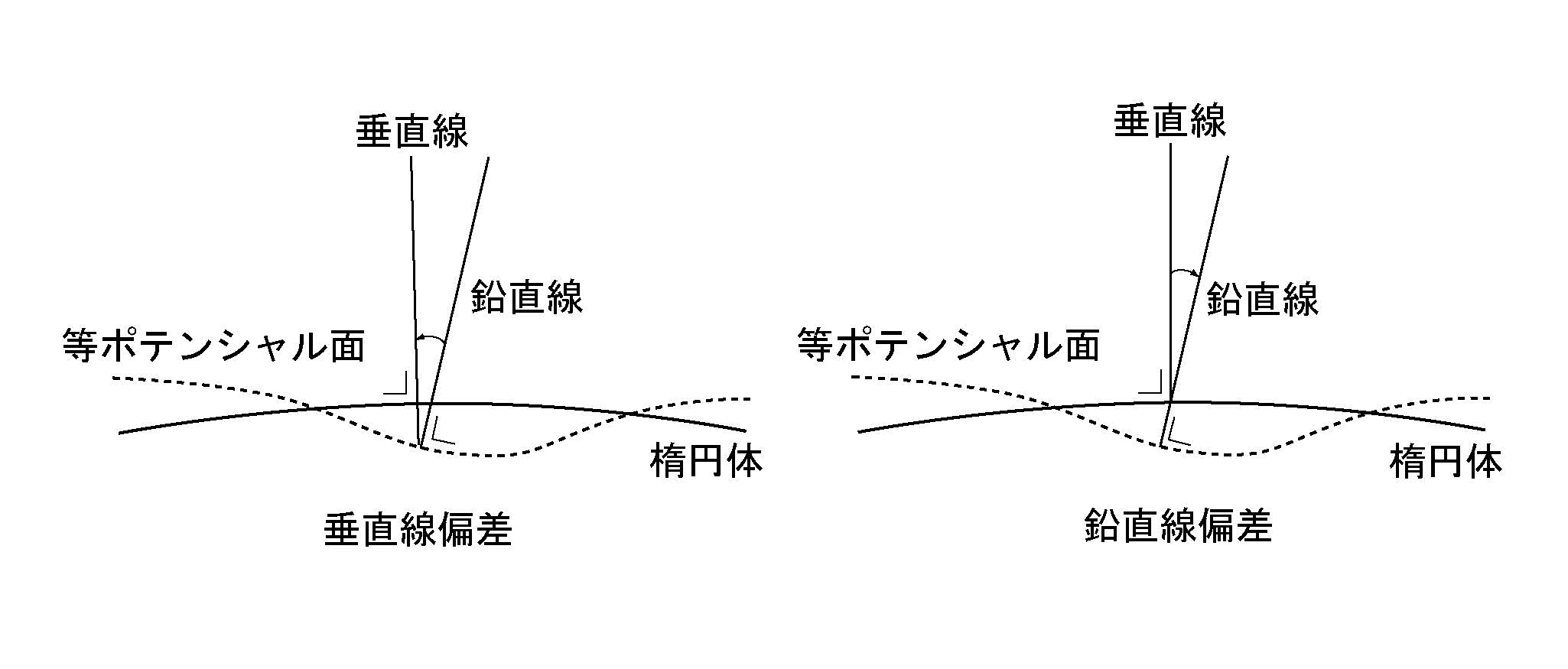
図8. 等ポテンシャル面に直交する鉛直線と楕円体に直交する垂直線. 鉛直線を基準にした垂直線のずれ(垂直線偏差)と垂直線を基準にした鉛直線のずれ(鉛直線偏差)は, 同量であると見なして差し支えない.
2-1-7. ジオイド, 高さ, 楕円体高(*)
さまざまな地表の形状をどのように表せばよいだろうか? 水は高いところから低いところへ流れる. これと逆の見方をすると, 水が静止している水平面は, いたるところ同じ高さである. 水平面を基準にして, これに垂直な方向, つまり重力と平行な方向の距離を測れば, 高さを表すことができるだろう.
実は, 高い低いを問わず, あらゆる場所に水平面を想定することができる. 物理学的には, 水平面とは, 重力のポテンシャルの値が等しい点を結んでできる等ポテンシャル面である. 値のとり方によって, 無数の等ポテンシャル面を描くことができる. このうち, 地球の形状を最も良く近似するものがジオイドである. ジオイドが具体的にどのようなポテンシャル値をとるか, 測地学では厳密に定義されている. 海洋は地表の約70%の面積を占めるので, ジオイドは平均海面にきわめて近い形をしている.
高さとは, ジオイドを基準にして, つねに等ポテンシャル面に垂直に測った距離と考えればよい(標高). これに対し, 楕円体に立てた垂線(垂直線)に沿って, 楕円体から地表まで測った距離を楕円体高と呼ぶ(図9). 水準測量では前者が, GPS測量では後者が決定される.
注意すべきことは, 地球内部の質量分布の不均質を反映して, 等ポテンシャル面の形が平坦でないことである. また, 隣り合う等ポテンシャル面も平行でない. 従って, 水準測量のみでは高さを決定できない.
ジオイドも凹凸を持っている. 楕円体を基準にしたジオイドの高さをジオイド高という. 全地球規模で, ジオイドはおよそ-105mから+85mの起伏を持つ.
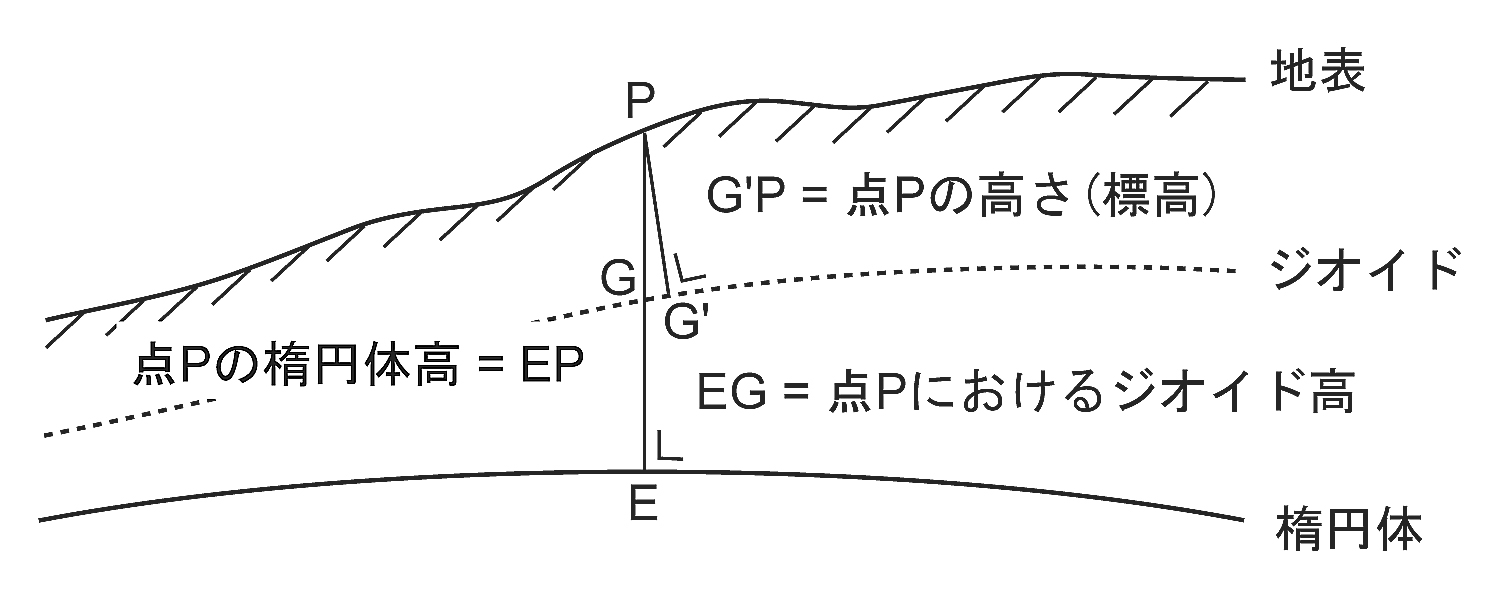
図9. 等ポテンシャル面に直交する鉛直線と楕円体に直交する垂直線. 鉛直線を基準にした垂直線のずれ(垂直線偏差)と垂直線を基準にした鉛直線のずれ(鉛直線偏差)は, 同量であると見なして差し支えない.
参考文献・関連Webサイト
- 宇津徳治(2001):地震学(第3版), 共立出版.
- 宇津徳治編(1997):地震の辞典, 朝倉書店.
- 国土地理院のホームページ内「日本の測地座標系」のページ