4-5. 地球の重力
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
4-5-1. 重力ポテンシャル
重力は, 地球の引力と自転による遠心力の合力である. このうち, 引力ポテンシャルは
\[ V=G\iiint\frac{\rho}{l}dv \tag{1} \]
であり, 遠心力は, 地球の自転角速度を$\omega$とすると
\[ f_x=\omega^2 x\\ f_y=\omega^2 y\\ f_z=0\\ |f|=\omega^2\sqrt{(x^2+y^2)} \tag{2} \]
であり,
\[ \Phi =\frac{1}{2} \omega^2(x^2+y^2) \tag{3} \]
とすると, $f=\mathrm{grad} \Phi =(\omega^2_x,\omega^2_y,0)$であるので, $\Phi$は遠心力のポテンシャルである.
従って, 重力ポテンシャル$W$は
\[ W=V+\Phi=G\iiint \frac{\rho}{l}dv + \frac{1}{2}\omega^2(x^2+y^2) \tag{4} \]
と表され, 重力ベクトルは
\[ {\bf g} = \mathrm{grad}W \tag{5} \]
であり, その絶対値$g=|g|$を重力の大きさ(あるいは単に重力)と呼ぶ.
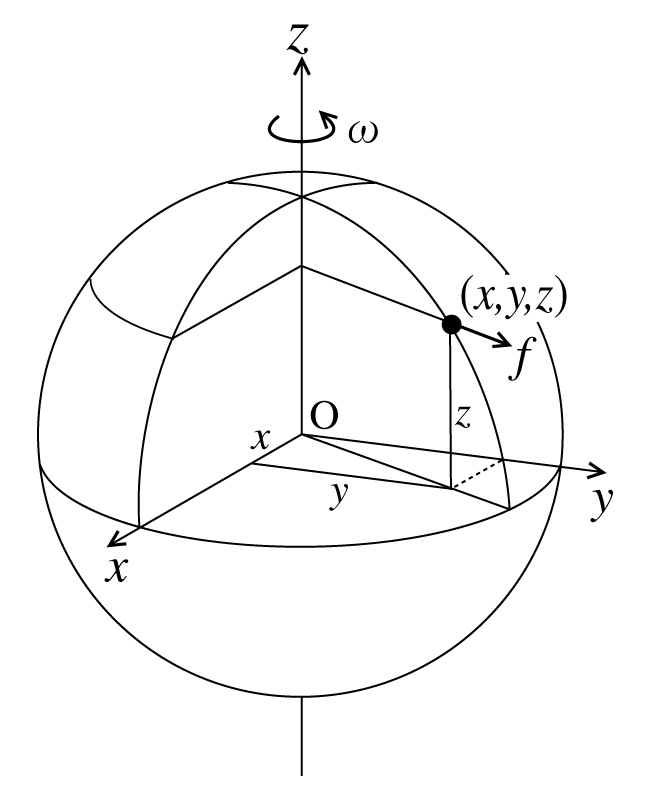
図1
4-5-2. 球面調和関数による引力ポテンシャル
引力ポテンシャル
\[ V=G\iiint \frac{dM}{l} \tag{6} \]
に改めて(24)式の
\[ \frac{1}{l}=\sum_{n=0}^{\infty}\frac{r'^n}{r^{n+1}}P_n(\cos{\psi}) \tag{7} \]
を代入すると
\[ V=G\sum_{n=0}^{\infty}\frac{1}{r^{n+1}}\iiint r'^n P_(\cos{\psi})dM \tag{8} \]
である.
一方, 点Pを地球の外部の点とすると$V$はラプラスの方程式$\nabla^{2}V=0$を満たすので
\[ V=\sum_{n=0}^{\infty}\frac{1}{r^{n+1}}Y_n(\theta,\lambda) \tag{9} \]
と書ける. ただし, $Y_n(\theta,\lambda)$は, $A_{nm}$, $B_{nm}$を実係数として,
\[ \begin{equation} \begin{array}{l} Y_n(\theta, \lambda)&=G\sum_{m=0}^{n}\left(A_{nm}R_{nm}(\theta,\lambda)+B_{nm}S_{nm}(\theta,\lambda) \right) \\ R_{nm}(\theta,\lambda)&=P_n^m(\cos{\theta})\cos{m\lambda} \\ S_{nm}(\theta,\lambda)&=P_n^m(\cos{\theta})\sin{m\lambda} \end{array} \end{equation} \tag{10}\]
である.
(8)式と, (9)式を比較し,
\[ Y_n(\theta,\lambda)=G\iiint r'^n P_n(\cos{\psi})dM \tag{11} \]
を得る.
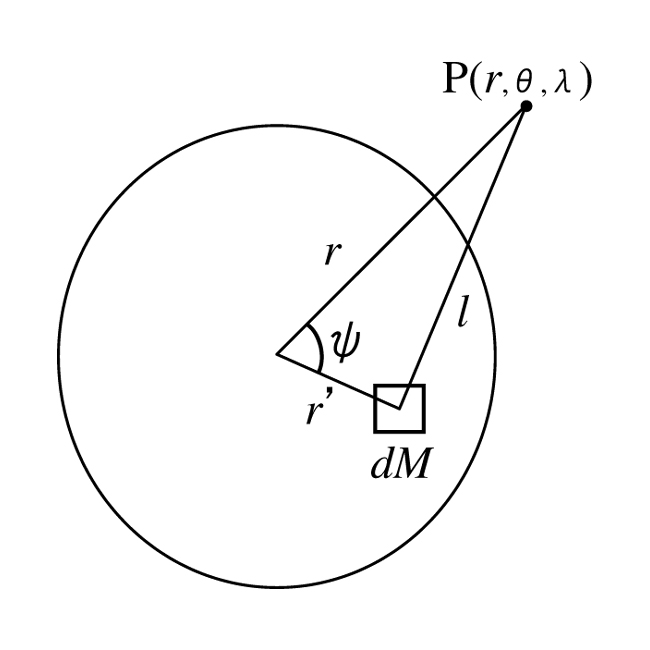
図2
4-5-3. 球面調和関数係数と質量分布
具体的に, $A_{nm}$ , $B_{nm}$ を求めるために, $\cos{\psi}$を$(\theta,\lambda)$で書き改めると, 球面調和関数の加法定理
\[ \begin{equation} \begin{array}{l} P_n(\cos{\psi})&=P_n(\cos{\theta})P_n(\cos{\theta '}) \\ &+2\sum_{m=1}^{n}\frac{(n-m)!}{(n+m)!}\left(R_{nm}(\theta,\lambda)R_{nm}(\theta',\lambda')+S_{nm}(\theta,\lambda)S_{nm}(\theta',\lambda') \right) \end{array} \end{equation} \tag{12} \]
を用いて
\[ Y_n(\theta,\lambda)=G\iiint r'^n\left\{ P_n P'_n +2\sum_{m=1}^{n}\frac{(n-m)!}{(n+m)!}(R_{nm}R'_{nm}+S_{nm}S'_{nm}) \right\}dM \tag{13} \]
であるので,
\[ \begin{equation} \begin{array}{rl} A_{n0}&=G\iiint P_n(\cos{\theta'})r'^n dM \\ \left[ \begin{array}{l} A_{nm} \\ B_{nm} \end{array} \right] &=2\frac{(n-m)!}{(n+m)!}G\iint r'^n\left[ \begin{array}{l} R_{nm}(\theta',\lambda') \\ S_{nm}(\theta',\lambda') \end{array} \right] dM \end{array} \end{equation} \tag{14} \]
を得る.
4-5-4. 球面調和関数係数の低次の項
$R_{nm}$, $S_{nm}$の低次(0-2次)の項を直交座標$x,y,z$で表すと,
\[ \begin{equation} \begin{array}{rlrl} R_{00}&=1 & S_{00}&=0 \\ rR_{10}&=z & rS_{10}&=0 \\ rR_{11}&=x & rS_{11}&=y \\ r^2R_{20}&=-\frac{1}{2}x^2-\frac{1}{2}y^2+z^2 & r^2S_{20}&=0 \\ r^2R_{21}&=3xz & r^2S_{21}&=3yz \\ r^2R_{22}&=3(x^2-y^2) & r^2S_{22}&=6xy \end{array} \end{equation} \tag{15} \]
となる. 従って, (14)式の0次の項は
\[ A_{00}=G\iiint dM=GM \tag{16} \]
であり, 地球の全質量Mが地球の重心にある場合(質点)の重力に一致する.
1次の項, 2次の項はそれぞれ
\[ A_{10}=G\iiint z' dM, , A_{11}=G\iiint x' dM, , B_{11}=G\iiint y' dM \tag{17} \]
\[ \begin{equation} \begin{array}{rl} A_{20}&=\frac{1}{2}G\iiint (-x'^2-y'^2+2z'^2) dM \\ A_{21}&=G\iiint x'z' dM \\ A_{22}&=\frac{1}{4}G\iiint (x'^2-y'^2) dM \\ B_{21}&=G\iiint y'z' dM \\ B_{22}&=\frac{1}{2}G\iiint x'y' dM \end{array} \end{equation} \tag{18} \]
である.
4-5-5. 慣性モーメントと慣性乗積
角速度$\omega$で回転している物体の角運動量$L$は
\[ \begin{equation} L=I{\bf \omega}=\left(\begin{array}{ccc} I_{xx}&I_{xy}&I_{xz} \\ I_{yx}&I_{yy}&I_{yz} \\ I_{zx}&I_{zy}&I_{zz} \end{array}\right) {\bf \omega} \end{equation} \tag{19} \]
である. ここで, 行列$I$は慣性テンソルであり, その成分のうち対角要素
\[ \begin{equation} \begin{array}{l} A=I_{xx}=\iiint(y'^2+z'^2)dM \\ B= I_{yy}=\iiint(z'^2+x'^2)dM \\ C= I_{zz}=\iiint(x'^2+y'^2)dM \\ \end{array} \end{equation} \tag{20} \]
を慣性モーメントと呼び, 非対角要素
\[ \begin{equation} \begin{array}{l} D=I_{xy}=I_{yx}=\iiint x'y'dM \\ E=I_{yz}=I_{zy}=\iiint y'z'dM \\ F=I_{zx}=I_{xz}=\iiint z'x'dM \\ \end{array} \end{equation} \tag{21} \]
を慣性乗積と呼ぶ.
これらを用いると, 球面調和関数係数(14)の2次の項は
\[ \begin{equation} \begin{array}{rl} A_{20}&=G\left( \frac{A+B}{2}-C \right) \\ A_{21}&=GF \\ A_{22}&=\frac{1}{4}G(B-A) \\ B_{21}&=GE \\ B_{22}&=\frac{1}{2}GD \end{array} \end{equation} \tag{22} \]
となる.
4-5-6. 禁止項
球面調和係数の低次の項のうち, 1次の項
\[ A_{10}=G\iiint z' dM, , A_{11}=\iiint x' dM, , B_{11}=G\iiint y' dM \tag{23} \]
は, 地球の重心を座標原点に選ぶことによりすべて0になる.
次に, 地球の自転軸は慣性主軸の1つとみなせるので, 地球の自転軸をz軸にとると, 2次の項のうち
\[ A_{21}=GF=0, , B_{21}=GE=0 \tag{24} \]
は, 自動的に0となる. これらの5項は禁止項(forbidden terms)と呼ばれている.
なお, 回転楕円体では, $A=B$ であるので, 2次の項としては
\[ A_{20}=G(A-C) \tag{25} \]
以外, すべて0となる.
4-5-7. 回転楕円体の重力ポテンシャル
回転楕円体の重力ポテンシャル$U$は, 地球の重力ポテンシャルと同様に, $V$を引力ポテンシャル, $\Phi$を遠心力ポテンシャルとして
\[ U=V+\Phi \tag{26} \]
で与えられる. 具体的に$U$を決めるためには, 回転楕円体の形$(a,f)$, 全 質量$M$, 回転角速度$\omega$を与えればよい. このとき, 楕円体面は等ポテン シャル面であるので, 楕円体上で$U$ は一定値, 楕円体の外で引力ポテンシャ ル$V$はラプラスの方程式の$\nabla2V=0$を満たすように$U$を決めることができ る.
いま, 楕円体座標$(u,\beta,\lambda)$を図10のように選ぶ. ここで, $u$は相似な楕円体の短軸半径, $\beta$は更成緯度, $\lambda$は経度で,
\[ E=\sqrt{a^2-u^2} \tag{27} \]
を焦点距離とすると, 直角座標との間に
\[ \begin{equation} \begin{array}{l} x=\sqrt{u^2+E^2}\sin{\theta}\cos{\lambda} \\ y=\sqrt{u^2+E^2}sin{\theta}\sin{\lambda} \\ z=u\sin{\beta} \end{array} \end{equation} \tag{28} \]
の関係がある.
楕円体座標でのラプラスの方程式の一般解は, $b$を地球の短軸半径, $Q_{nm}$を 第2種ルジャンドル関数として
\[ \begin{equation} \begin{array}{l} V(u,\beta,\gamma)=\sum_{n=0}^{\infty}\sum_{m=0}^{\infty}\frac{Q_n^m\left(i\frac{u}{E}\right)}{Q_n^m\left(i\frac{b}{E}\right)}(a_{nm}\cos{m\lambda}+b_{nm}\sin{m \lambda})P_n^m(\sin\beta) \\ ただし, \\ Q_n(t)=Q_n^0=\frac{1}{2}P_n(t)\ln{\frac{1+t}{1-t}}-\sum_{k=1}^{n}\frac{1}{k}P_{k-1}(t)P_{n-k}(t) \\ Q_n^m(t)=(1-t^2)^\frac{m}{2} \frac{d^mQ_n(t)}{dt^m} \tag{29} \end{array} \end{equation} \]
で与えられる.
回転楕円体では, $\gamma$方向, 赤道に対する対称性を考慮すると, $m=0$, $n=(偶数)$の項のみ 残ることがわかる. これらを考慮し, さらに遠心力ポテンシャル$\Phi$を加えると
\[ U=V+\Phi=\sum_{n=0}^{\infty}\frac{Q_{2n}\left(i\frac{u}{E}\right)}{Q_{2n}\left(i\frac{b}{E}\right)}a_{2n}P_{2n}(\sin\beta)+\frac{1}{2}\omega^2(u^2+E^2)\cos^2\beta \tag{30}\]
を得る.
次に, $a_{2n}$を決めるために, $U$が$u=b$(楕円体上)で一定値$U=U_0$の境界条件を 与えると
\[ a_0=U_0-\frac{1}{3}\omega^2a^2, a_2=\frac{1}{3}\omega^2a^2, a_{2n}=0 (n > 2) \tag{31} \]
であり, 最終的に$U_0$を$GM$で書き改めると
\[ U(u, \beta)=\frac{GM}{E}\tan^{-1}{\frac{E}{u}}+\frac{1}{2}\omega^2a^2\frac{q}{q_0}\left(\sin^2{\beta}-\frac{1}{3}\right)+\frac{1}{2}\omega^2(u^2+E^2)\cos^2{\beta} \tag{32} \]
ただし
\[ \begin{equation} \begin{array}{l} q=\frac{1}{2}\left[\left(1+3\frac{u^2}{E^2}\right)\tan^{-1}\frac{E}{u}-3\frac{u}{E}\right] \\ q_0=\frac{1}{2}\left[\left(1+3\frac{b^2}{E^2}\right)\tan^{-1}\frac{E}{b}-3\frac{b}{E}\right] \tag{33} \end{array} \end{equation} \]
を得る.
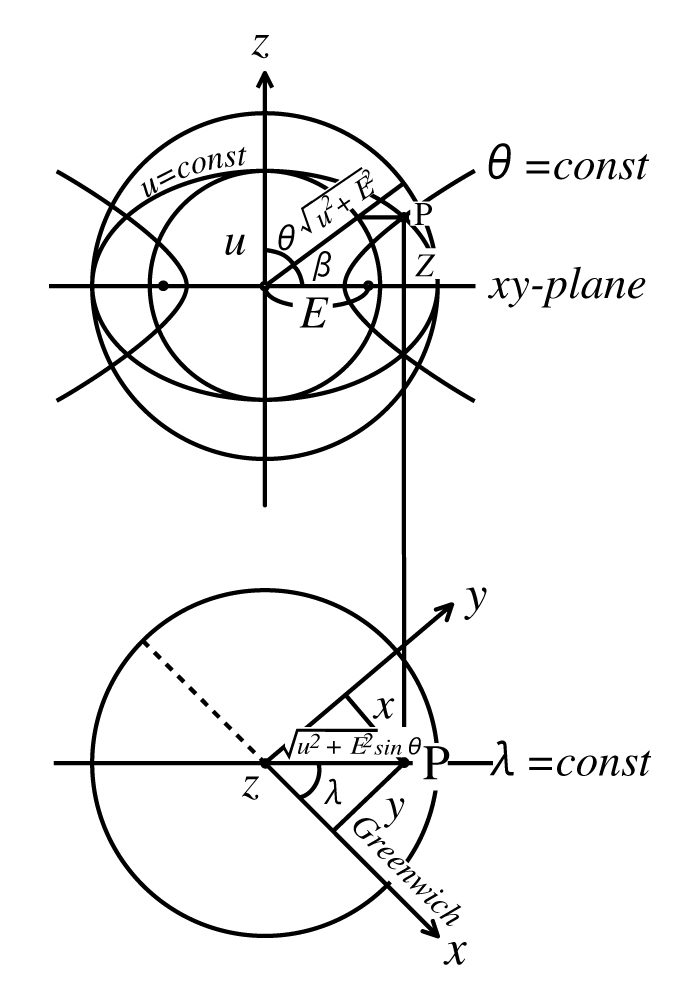
図3
4-5-8. 回転楕円体の重力
回転楕円体の重力$\gamma$ を正規重力 (normal gravity) と呼び, $U$ の勾配
\[ \begin{equation} \begin{array}{l} \boldsymbol{\gamma}=\mathrm{grad} U \\ \gamma=|\boldsymbol{\gamma}| \tag{34} \end{array} \end{equation} \]
で求めることができて
\[ \gamma=\frac{a\gamma_acos^2\psi+a\gamma_b\sin^2\psi}{\sqrt{a^2\cos^2{\psi}+b^2\sin^2{\psi}}} \tag{35} \]
(Somigliana, 1929)
$\phi$: 測地緯度, $\gamma a$: 赤道上での標準重力, $\gamma b$: 極での標準重力
を得る.
4-5-9. 球座標による回転楕円体の重力ポテンシャル
(32)式を座標変換して球座標で表すと
\[ U=\frac{GM}{r}\left[ 1+\sum_{n=1}^{\infty}\left(\frac{a}{r}\right)^{2n}\overline{A_{2n}} , \overline{P_{2n}}(\sin\phi) \right] + \frac{1}{2}\omega^2 r^2 \cos^2 \phi \tag{36} \]
を得る. ただし,
\[ \begin{equation} \begin{array}{l} \overline{A_{2n}}=\frac{(-1)^n}{2n+1}e^{2n}\left(1-\frac{2n}{2n+3}\frac{me'}{3q_0}\right) \cdot \frac{1}{\sqrt{4n+1}} \\ m=\frac{\omega^2a^2b}{GM} \\ q_0=\frac{1}{2}\left[ \left(1+3\frac{b^2}{E^2}\right)\tan^{-1}\frac{E}{b}-3\frac{b}{E} \right] \\ E=ae \tag{37} \end{array} \end{equation} \]
である.

